Types of Number Systems #
Decimal Numbers #
The number system that we use in our day-to-day life is the decimal number system. The decimal number system has base or radix 10 as it uses 10 digits from 0 to 9
For fractional decimal numbers, the column weights are negative powers of ten that decrease from left to right: 102 101 100. 10-1 10-2 10-3 10-4 …
Example: Express the number 480.52 as the sum of values of each digit.
Solution: 480.52 = (4 × 102) + (8 × 101) + (0 × 100) + (5 × 10-1) + (2 × 10-2)
Binary Numbers #
Uses two digits, 0 and 1.
Also called base 2 number system
Each position in a binary number represents a 0 power of the base (2). Example 20
Last position in a binary number represents a × power of the base (2). Example 2x where x represents the last position – 1.
EXAMPLE
Binary Number: 101012
Calculating Decimal Equivalent:
| Step | Binary Number | Decimal Number |
| Step 1 | 101012 | ((1 × 24) + (0 × 23) + (1 × 22) + (0 × 21) + (1 × 20))10 |
| Step 2 | 101012 | (16 + 0 + 4 + 0 + 1)10 |
| Step 3 | 101012 | 2110 |
Note: 101012 is normally written as 10101.
For fractional binary numbers, the column weights are negative powers of two that decrease from left to right:
22 21 20. 2-1 2-2 2-3 2-4 …
Hexadecimal Numbers #
Uses 10 digits and 6 letters: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
Letters represents numbers starting from 10. A = 10. B = 11, C = 12, D = 13, E = 14, F = 15.
Also called base 16 number system
Each position in a hexadecimal number represents a 0 power of the base (16). Example 160
Last position in a hexadecimal number represents a x power of the base (16). Example 16x where x represents the last position – 1.
EXAMPLE
Hexadecimal Number: 19FDE16
Calculating Decimal Equivalent:
| Step | Binary Number | Decimal Number |
| Step 1 | 19FDE16 | ((1 × 164) + (9 × 163) + (F × 162) + (D × 161) + (E × 160))10 |
| Step 2 | 19FDE16 | ((1 × 164) + (9 × 163) + (15 × 162) + (13 × 161) + (14 × 160))10 |
| Step 3 | 19FDE16 | (65536+ 36864 + 3840 + 208 + 14)10 |
| Step 4 | 19FDE16 | 10646210 |
Note: 19FDE16 is normally written as 19FDE.
Octal Numbers #
Uses eight digits, 0,1,2,3,4,5,6,7.
Also called base 8 number system
Each position in a octal number represents a 0 power of the base (8). Example 80
Last position in a octal number represents a × power of the base (8). Example 8x where x represents the last position – 1.
EXAMPLE
Octal Number: 125708
Calculating Decimal Equivalent:
| Step | Octal Number | Decimal Number |
| Step 1 | 125708 | ((1 × 84) + (2 × 83) + (5 × 82) + (7 × 81) + (0 × 80))10 |
| Step 2 | 125708 | (4096 + 1024 + 320 + 56 + 0)10 |
| Step 3 | 125708 | 549610 |
Note: 125708 is normally written as 12570.
Number system conversions #
Any numbering system can be summarized by the following relationship:
| N = bi qi | ||
| where: | N is a real positive number i.e Decimal b is the digit q is the base value i is integer representing position can be positive, negative or zero |
|
N = bn qn… b3 q3 + b2 q2 + b1 q1 + b0 q0 + b-1 q-1 + b-2 q-2… etc.
EX: (23.45)5 = 2X51 + 3X50 + 4X5-1 + 5X5-2 = 14
Binary -to-Decimal Conversions (base 2 to base 10) #
The decimal equivalent of a binary number can be determined by adding the column values of all of the bits that are 1 and discarding all of the bits that are 0.
Example: Convert the binary number 100101.01 to decimal.
Solution: Start by writing the column weights; then add the weights that correspond to each 1 in the number.
25 24 23 22 21 20. 2-1 2-2
32 16 8 4 2 1. ½ ¼
1 0 0 1 0 1. 0 1
32 +4 +1 +¼ = 37¼
Example: convert (1000100)2 to decimal
= 64 + 0 + 0+ 0 + 4 + 0 + 0
= (68)10
Decimal-to-Binary Conversions (base 10 to base 2) #
Write the decimal weight of each column and place 1’s in the columns that sum to the decimal number.
Example: Convert the decimal number 49 to binary.
26 25 24 23 22 21 20.
64 32 16 8 4 2 1.
0 1 1 0 0 0 1.
Write 1 from MSB such that sum adds up to 49
Another method
Example: convert (68)10 to binary
Solution:
68/2 = 34 remainder is 0
34/ 2 = 17 remainder is 0
17 / 2 = 8 remainder is 1
8 / 2 = 4 remainder is 0
4 / 2 = 2 remainder is 0
2 / 2 = 1 remainder is 0
1 / 2 = 0 remainder is 1
Answer = 1 0 0 0 1 0 0
Note: the answer is read from bottom (MSB) to top (LSB) as 10001002
Decimal fraction-to-Binary fraction Conversions #
You can convert a decimal fraction to binary by repeatedly multiplying the fractional results of successive multiplications by 2. The carries form the binary number.
Example: Convert the decimal fraction 0.188 to binary by repeatedly multiplying the fractional results by 2.
| Solution: 0.188 × 2 = 0.376 carry = 0 MSB
0.376 × 2 = 0.752 carry = 0 0.752 × 2 = 1.504 carry = 1 0.504 × 2 = 1.008 carry = 1 0.008 × 2 = 0.016 carry = 0 LSB Answer = .00110 (for five significant digits) |
Example: convert (0.68)10 to binary fraction.
Solution: 0.68 × 2 = 1.36 integer part is 1
0.36 × 2 = 0.72 integer part is 0
0.72 × 2 = 1.44 integer part is 1
0.44 × 2 = 0.88 integer part is 0
Answer = 0. 1 0 1 0…..
Example: convert (68.68)10 to binary equivalent.
Answer = 1 0 0 0 1 0 0 . 1 0 1 0….
Converting Binary to Hex and Octal #
Conversion of binary numbers to octal and hex simply requires grouping bits in the binary numbers into groups of three bits for conversion to octal and into groups of four bits for conversion to hex.
Groups are formed beginning with the LSB and progressing to the MSB.
Thus, 11 100 1112 = 3478 1110 01112 = E716
11 100 010 101 010 010 0012 = 30252218 1 1000 1010 1000 01112 = 18A8716
1.2.5 Converting Hex To Decimal (base 16 to base 10)
Example: Express 1A2F16 in decimal and binary.
Solution: Start by writing the column weights:
4096 256 16 1
1 A 2 F
1(4096) + 10(256) +2(16) +15(1) = 670310
Example: convert (F4C)16 to decimal
= (F × 162) + (4 × 161) + (C × 160)
= (15 × 256) + (4 × 16) + (12 × 1)
1.2.6 Converting Octal To Decimal (base 8 to base 10)
Example: Express 37028 in decimal
Solution: Start by writing the column weights:
512 64 8 1
3 7 0 2
3(512) + 7(64) +0(8) +2(1) = 198610
1.2.7 Converting Decimal To Hex (base 10 to base 16)
Example: convert (4768)10 to hex.
Solution: Start by dividing with 16
= 4768 / 16 = 298 remainder 0
= 298 / 16 = 18 remainder 10 (A)
= 18 / 16 = 1 remainder 2
= 1 / 16 = 0 remainder 1
Answer: 1 2 A 0 = (12A0)16
Note: the answer is read from bottom to top, same as with the binary case.
= 3840 + 64 + 12 + 0
= (3916)10
1.2.8 Converting Decimal To Octal (base 10 to base 8)
Example: convert (177)10 to octal
Solution: Start by dividing with 16
177 / 8 = 22 remainder is 1
22 / 8 = 2 remainder is 6
2 / 8 = 0 remainder is 2
Answer = 2 6 1 = (261)8
Note: the answer is read from bottom to top as (261)8, the same as with the binary case.
Conversion of decimal fraction to octal fraction is carried out in the same manner as decimal to binary except that now the multiplication is carried out by 8. To convert octal to hex first convert octal to binary and then convert binary to hex. To convert hex to octal first convert hex to binary and then convert binary to octal.
Complements of Binary Numbers #
1’s Complement #
The 1’s complement of a binary number is just the inverse of the digits. To form the 1’s complement, change all 0’s to 1’s and all 1’s to 0’s.
For example, the 1’s complement of 11001010 is 00110101
In digital circuits, the 1’s complement is formed by using inverters:

2’s Complement: #
The 2’s complement of a binary number is found by adding 1 to the LSB of the 1’s complement.
Recall that the 1’s complement of 11001010 is
00110101 (1’s complement)
To form the 2’s complement, add 1: +1
00110110 (2’s complement)
Tip: To find 2’s compliment directly copy LSB to answer if it is 0 copy next LSB and so on till you get 1. After copying 1 do 1’s compliment of rest of MSB
General “b’s Complement” Numbers for Base b and Base 2 #
Everything flows in general the same as above except for the changes shown in the table below. In this table, “b” in column 2 represents a general base b number. Column 3 represents binary numbers.
Row 2 gives the representation of the number -1 (with leading digits equal to b-1, b the base).
Row 3 gives the equation for complementing each of the digits (in each case, subtract the digit from b-1, b the base)
Row 4 gives examples of positive numbers (with leading zeros extending leftward to infinity).
Row 5 shows the complement of the number in row 4 (and shows that the sum of the two equals zero)
| Base10’s (base – 1) = 10 – 1 = 9 |
Base b
(base – 1) = (b – 1) = B |
Base 2
(base – 1) = (2 – 1) = 1 |
|
| Number = -1 | 9999…….99999 | bbbbbb…..bbbb | 1111….1111 |
| Complement of digit | |||
| Example of 8 digit positive
number (leading 0 required) |
00034857 | For base 5, as an example,
00340240 |
01011010 |
| Example of 8 digit negative
number (leading (b-1) required) with magnitude equal to positive number in row above |
00034857 -> 99965143
00034857 00000000 |
00340240 -> 44104210
00340240 00000000 |
01011010 -> 10100110
01011010 +10100110 00000000 |
Arithmetic for various number system #
Binary Addition #
The rules for binary addition are:
0 + 0 = 0 Sum = 0, carry = 0
0 + 1 = 1 Sum = 1, carry = 0
1 + 0 = 1 Sum = 1, carry = 0
1 + 1 = 10 Sum = 0, carry = 1
When an input (carry = 1) due to a previous result, the rule is:
1 + 1 + 1 = 11 Sum = 1, carry = 1
Example: Add the binary numbers 00111 and 10101 and show the equivalent decimal addition
Solution: 111
00111 7
10101 21
11100 28
Binary Subtraction #
The rules for binary subtraction are:
0 – 0 = 0
1 – 1 = 0
1 – 0 = 1
10 – 1 = 1 with a borrow of 1
Example: Subtract the binary number 00111 from 10101 and show the equivalent decimal subtraction.
Solution: 111
10101 21
00111 7Hexadecimal Addition
Examples
Carry 0 00 00
Addend 3B2 3B2 3B2 3B2
Augend + 41C + 41C + 41C + 41C
Sum E CE 7CE
Carry 1 1 1 1
Addend A27 A27 A27 A27 A27
Augend + C3B + C3B + C3B + C3B + C3B
Sum 2 62 662 1662
Hexadecimal Subtraction #
Uses the same principle of “borrowing” that decimal and binary subtraction uses.
Example
borrow
Minuend 6E 6E 6E
Subtrahend – 29 – 29 -29
Difference 5 45
Minuend AC3 AC3 AC3 AC3
Subtrahend – 604 – 604 – 604 – 604
Difference F BF 4BF
Octal Addition #
Examples
carry 1
Addend 127 127 127 127
Augend + 42 + 42 + 42 + 42
Sum 1 71 171
carry 1 11 11 1
Addend 1777 1777 1777 1777 1777
Augend +777 + 777 + 777 + 777 + 777
Sum 6 76 776 2776
Octal Subtraction #
This is performed exactly like binary and decimal subtraction with the borrowing technique. Whenever the subtrahend is larger than the minuend, a 1 is borrowed from the next column.
Example
Minuend 124 124 124
Subtrahend – 63 – 63 -63
Sum 1 41
Signed Binary Numbers #
There are several ways to represent signed binary numbers. In all cases, the MSB in a signed number is the sign bit, that tells you if the number is positive or negative.
Computers use a modified 2’s complement for signed numbers. Positive numbers are stored in true form (with a 0 for the sign bit) and negative numbers are stored in complement form (with a 1 for the sign bit).
For example, the positive number 58 is written using 8-bits in true (un-complemented) as:
00111010 (true form).
Sign bit
Magnitude bits
Negative numbers are written as the 2’s complement of the corresponding positive number.
The negative number -58 is written as:
11000110 (complement form)
Sign bit
Magnitude bits
An easy way to read a signed number that uses this notation is to assign the sign bit a column weight of -128 (for an 8-bit number). Then add the column weights for the 1’s.
Example: Assuming that the sign bit = -128, show that 11000110 = -58 as a 2’s complement signed number.
Solution: Column weights -128 64 32 16 8 4 2 1.
1 1 0 0 0 1 1 0
-128 +64 +4 +2 = -58
1.5 Arithmetic Operations with Signed Numbers #
1.5.1 Addition #
Using the signed number notation with negative numbers in 2’s complement form simplifies addition and subtraction of signed numbers.
Rules for addition: Add the two signed numbers. Discard any final carries. The result is in signed form.
Examples:
00011110 = +30 00001110 = +14 11111111 = -1
00001111 = +15 11101111 = -17 11111000 = -8
Discard Final carry
00101101 = 45 11111101 = -3 1 11110111 = -9
Overflow Condition #
When two numbers are added and the number of bits required to represent the sum exceeds the number of bits in the two numbers, an overflow results as indicated by an incorrect sign bit. An overflow can occur only when both numbers have the same sign.
Two examples are:
01000000 = +128 10000001 = -127
01000001 = +129 10000001 = -127
Discard carry
Wrong! The answer is incorrect and the sign bit has changed
10000001 = -126 100000010 = -2
Subtraction #
Rules for subtraction: 2’s complement the subtrahend and add the numbers. Discard any final carries. The result is in signed form.
Examples:
00011110 = +30 11111111 = -1
11110001 = -15 00001000 = +8
Discard Final carry
Discard Final carry
1 00001111 = +15 1 00000111 = +7
Multiplication and division is carried out by repetitive addition and subtraction
Floating Point Numbers #
Floating point notation is capable of representing very large or small numbers by using a form of scientific notation. A 32-bit single precision number is illustrated:
| S | E (8 bits) | F (23 bits) |
Sign bit Biased exponent (+127) Magnitude with MSB dropped
Example: Express the speed of light, c, in single precision floating point notation.
(c = 0.2998 x 109)
Solution:
Binary: c = 0001 0001 1101 1110 1001 0101 1100 00002
Scientific notation: c = 1.001 1101 1110 1001 0101 1100 0000 × 228
Floating point notation:
| 0 | 10011011 | 001 1101 1110 1001 0101 1100 |
S = 0 because the number is positive.
E = 28 + 127 = 15510 = 1001 10112.
F = the next 23 bits after the first 1 is dropped
Binary Codes #

Binary coded decimal (BCD) #Binary coded decimal (BCD) is a weighted code that is commonly used in digital systems when it is necessary to show decimal numbers such as in clock displays. The table illustrates the difference between straight binary and BCD. BCD represents each decimal digit with a 4-bit code. Notice that the codes 1010 through 1111 are not used in BCD. |
|
||||||
Gray code #Gray code is an unweighted code that has a single bit change between one code word and the next in a sequence. Gray code is used to avoid problems in systems where an error can occur if more than one bit changes at a time. A shaft encoder is a typical application. Three IR emitter/detectors are used to encode the position of the shaft. The encoder on the left uses binary and can have three bits change together, creating a potential error. The encoder on the right uses gray code and only 1-bit changes, eliminating potential errors. |
|
Binary-to-Gray Conversion #
Following is algorithm to convert a binary value to its corresponding standard Gray code value :
- Retain the MSB.
- From left to right, add each adjacent pair of binary code bits to get the next Gray code bit, discarding the carry.
The following example shows the conversion of binary number (10110)2 to its corresponding standard Gray code value, (11101)Gray.

Gray-to-Binary Conversion #
The algorithm to convert a standard Gray code value to its corresponding binary value is as follows:
- Retain the MSB.
- From left to right, add each binary code bit generated to the Gray code bit in the next position, discarding the carry.
The following example shows the conversion of the standard Gray code value (11011)Gray to its corresponding binary value, (10010)2.
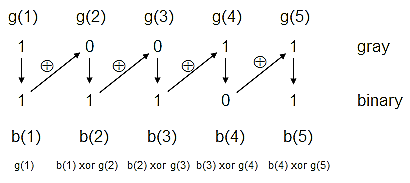
Standard Circuit for binary to gray

Gray to binary
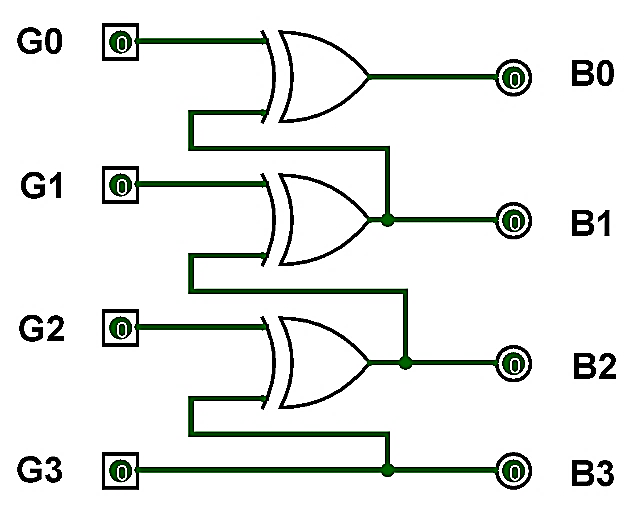
Excess-3 Code #
The Excess-3 code uses a bias value of three. It means we have to add 3(0011) to the corresponding BCD code. Hence the codes for the ten digits 0, 1, …, 9 are 0011, 0100, …, 1100 respectively. The decimal number 294 would be represented as 0101 1100 0111.
84-2-1 Code #
The 84-2-1 code uses the weights of 8, 4, -2 and -1 in the coding. The decimal number 294 would be represented as 0110 1111 0100.
2421 Code #
The 2421 code uses the weights of 2, 4, 2 and 1 in the coding. According to the weights, certain digits may have alternative codes. For instance, the digit 3 could be represented as 0011 or 1001. However, we pick the former in the standard 2421 coding, so that the codes for the first five digits 0 – 4 begin with 0, whereas the codes for the last five digits 5 – 9 begin with 1. The decimal number 294 would be represented as 0010 1111 0100.
ASCII Code #
ASCII is a code for alphanumeric characters and control characters. In its original form, ASCII encoded 128 characters and symbols using 7-bits. The first 32 characters are control characters, that are based on obsolete teletype requirements, so these characters are generally assigned to other functions in modern usage.
In 1981, IBM introduced extended ASCII, which is an 8-bit code and increased the character set to 256. Other extended sets (such as Unicode) have been introduced to handle characters in languages other than English.
Error Detection #
- Transmitted binary information is subject to noise that could change bits 1 to 0 and vice versa
- An error detection code is a binary code that detects digital errors during transmission
- The detected errors cannot be corrected, but can prompt the data to be retransmitted
- The most common error detection code used is the parity bit
- A parity bit is an extra bit included with a binary message to make the total number of 1’s either odd or even
| Message xyz | P(odd) | P(even) |
| 000 | 1 | 0 |
| 001 | 0 | 1 |
| 010 | 0 | 1 |
| 011 | 1 | 0 |
| 100 | 0 | 1 |
| 101 | 1 | 0 |
| 110 | 1 | 0 |
| 111 | 0 | 1 |
- The P(odd) bit is chosen to make the sum of 1’s in all four bits odd
- The even-parity scheme has the disadvantage of having a bit combination of all 0’s
- Procedure during transmission:
- At the sending end, the message is applied to a parity generator
- The message, including the parity bit, is transmitted
- At the receiving end, all the incoming bits are applied to a parity checker
- Any odd number of errors are detected
- Parity generators and checkers are constructed with XOR gates (odd function)
- An odd function generates 1 iff an odd number if input variables are 1
| S
Sign bit |
E (8 bits)
Biased exponent (+127) |
F (23 bits)
Magnitude |
Summary #
- To convert binary to decimal Start by writing the column weights; then adds the weights that correspond to each 1 in the number.
- To convert decimal to any number system, divide by base of that number system and reminders from bottom to top will be answer.
- To convert decimal fraction to any number system, multiply by base of that number system and carry from top to bottom will be answer.
- Binary to hex/octal can be converted by grouping 4/3 bits and writing equivalent hex/octal digits.
- Hex/octal to binary can be converted by writing 4/3 bit binary value corresponding to each digit.
- The 1’s complement of a binary number is just the inverse of the digits
- The 2’s complement of a binary number is 1’s complement+1. It represent negative number in signed arithmetic i.e. 2’s compliment of +8 in binary gives -8.
- In signed number MSB is 0 for positive number and 1 for negative number
- Floating point numbers
- Binary-to-Gray conversion: Retain the MSB. From left to right, add each adjacent pair of binary code bits to get the next Gray code bit, discarding the carry.
- Gray-to-Binary Conversion: Retain the MSB. From left to right, add each binary code bit generated to the Gray code bit in the next position, discarding the carry.
- Excess-3 code uses a bias value of three. i.e. Excess-3 = BCD+0011




